Insiemi numerabili
Uno dei primi risultati ottenuti da Cantor nella sua investigazione del concetto di infinito è la dimostrazione della numerabilità dell'insieme dei numeri razionali. Vediamo cosa vuol dire questa strana cosa, partendo proprio dall'inizio. (In questa sezione considererò elementari i concetti di insieme e di appartenenza ad un insieme. Altri concetti verranno di volta in volta chiariti con delle note.)
Concetto di numerabilità
Consideriamo un insieme finito F ed un suo sottoinsieme proprio A. È ovvio che A 'contiene meno elementi' di F, cosa che si indica con:
card(F) > card(A)
Questa ovvietà non è più tale, anzi in un ben preciso senso è falsa, quando si parla di insiemi che
contengono un numero infinito di elementi (e qui si nega la 'nozione comune'
di Euclide per cui 'il tutto è maggiore della parte'). Consideriamo ad esempio
l'insieme 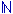 dei numeri naturali
(0,1,2,3,...). Non esiste alcun numero finito che rappresenti la cardinalità
di
dei numeri naturali
(0,1,2,3,...). Non esiste alcun numero finito che rappresenti la cardinalità
di  e si adotta allora per questo
concetto il simbolo
e si adotta allora per questo
concetto il simbolo 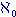 (aleph
zero, dove 'aleph' è la prima lettera dell'alfabeto ebraico. Il motivo per
cui non si utilizza il 'normale' simbolo di infinito
(aleph
zero, dove 'aleph' è la prima lettera dell'alfabeto ebraico. Il motivo per
cui non si utilizza il 'normale' simbolo di infinito  apparirà chiaro in seguito, quando si parlerà degli
insiemi non numerabili). Si pone quindi, per definizione:
apparirà chiaro in seguito, quando si parlerà degli
insiemi non numerabili). Si pone quindi, per definizione:
card( ) =
) = 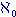 .
.
Consideriamo ora un sottoinsieme proprio di  , ad esempio l'insieme A dei quadrati. È ovvio che anche A contiene
infiniti elementi, anche se non TUTTI i numeri interi sono in A. Basandosi sul
fatto che ad ogni n
, ad esempio l'insieme A dei quadrati. È ovvio che anche A contiene
infiniti elementi, anche se non TUTTI i numeri interi sono in A. Basandosi sul
fatto che ad ogni n
 si può associare uno ed un solo a
si può associare uno ed un solo a A, e precisamente tramite la
relazione a=n2, Cantor conclude che l'insieme dei
quadrati è equivalente a quello dei
numeri naturali, cioè pone:
A, e precisamente tramite la
relazione a=n2, Cantor conclude che l'insieme dei
quadrati è equivalente a quello dei
numeri naturali, cioè pone:
card(A)=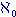 .
.
In generale, Cantor considera un insieme infinito A equivalente ad un altro
insieme infinito B, quando ad ogni elemento di A è possibile far corrispondere
uno ed un solo elemento di B (cioè quando esiste una relazione
biunivoca tra A e B).
In particolare, Cantor considera un insieme
infinito A equivalente all'insieme infinito dei numeri naturali  , quando ad ogni elemento di A è possibile far
corrispondere uno ed un solo elemento di
, quando ad ogni elemento di A è possibile far
corrispondere uno ed un solo elemento di  . Quando esiste una tale relazione biunivoca tra gli elementi di A e
gli elementi di
. Quando esiste una tale relazione biunivoca tra gli elementi di A e
gli elementi di  si dice che l'insieme A
è numerabile. (Si considera numerabile anche un insieme
finito).
si dice che l'insieme A
è numerabile. (Si considera numerabile anche un insieme
finito).
È un gioco da ragazzi dimostrare che, ad esempio, l'insieme dei
numeri pari è numerabile, come pure quello dei numeri primi o l'insieme dei
numeri relativi (positivi e negativi) o - in generale - ogni sottoinsieme di
 .
.
Numerabilità dell'insieme dei
numeri razionali
Viene da chiedersi se esistono
insiemi NON numerabili. Un primo candidato naturale sembra essere l'insieme
 dei numeri razionali, cioè dei numeri
della forma m/n, con m ed n interi (ed n diverso da zero). In effetti
tra due numeri razionali qualsiasi esistono infiniti altri numeri razionali, proprietà
questa non condivisa né dall'insieme dei numeri naturali né da alcun suo
sottoinsieme.
dei numeri razionali, cioè dei numeri
della forma m/n, con m ed n interi (ed n diverso da zero). In effetti
tra due numeri razionali qualsiasi esistono infiniti altri numeri razionali, proprietà
questa non condivisa né dall'insieme dei numeri naturali né da alcun suo
sottoinsieme.
Ora, anche se  sembra
contenere 'molti' più elementi di
sembra
contenere 'molti' più elementi di  ,
Cantor riesce a dimostrare che in effetti:
,
Cantor riesce a dimostrare che in effetti:
card( ) =
) = 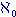 .
.
Per la dimostrazione originale
di Cantor, vedi qui,
dove c'è quella strana tabella piena di frecce. Io propongo un mio modo
(credo semplice) di dimostrare questo fatto. Se associo al numero razionale m/n il numero intero che si ottiene facendo
seguire alla rappresentazione decimale di
'm' un 'A' e poi la rappresentazione decimale di 'n' (ad esempio, a 17/8
associo 17A8), rappresento ogni numero razionale con un numero intero
scritto in notazione esadecimale, e sono anche certo che a razionali diversi
associo interi diversi. Ora ho posto in
relazione biunivoca  con un sottoinsieme
proprio S di
con un sottoinsieme
proprio S di  . Per la precisione, S è
composto da quegli interi che nella loro rappresentazione esadecimale hanno
solo cifre più un unico 'A' (che non deve stare né al primo né all'ultimo
posto). È evidente che S, essendo un sottoinsieme di
. Per la precisione, S è
composto da quegli interi che nella loro rappresentazione esadecimale hanno
solo cifre più un unico 'A' (che non deve stare né al primo né all'ultimo
posto). È evidente che S, essendo un sottoinsieme di  , è numerabile. Quindi anche l'insieme dei
numeri razionali, equivalente ad S, è numerabile.
, è numerabile. Quindi anche l'insieme dei
numeri razionali, equivalente ad S, è numerabile.
 dei numeri naturali
(0,1,2,3,...). Non esiste alcun numero finito che rappresenti la cardinalità
di
dei numeri naturali
(0,1,2,3,...). Non esiste alcun numero finito che rappresenti la cardinalità
di  e si adotta allora per questo
concetto il simbolo
e si adotta allora per questo
concetto il simbolo 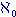 (aleph
zero, dove 'aleph' è la prima lettera dell'alfabeto ebraico. Il motivo per
cui non si utilizza il 'normale' simbolo di infinito
(aleph
zero, dove 'aleph' è la prima lettera dell'alfabeto ebraico. Il motivo per
cui non si utilizza il 'normale' simbolo di infinito  apparirà chiaro in seguito, quando si parlerà degli
insiemi non numerabili). Si pone quindi, per definizione:
apparirà chiaro in seguito, quando si parlerà degli
insiemi non numerabili). Si pone quindi, per definizione:
 dei numeri razionali, cioè dei numeri
della forma m/n, con m ed n interi (ed n diverso da zero). In effetti
tra due numeri razionali qualsiasi esistono
dei numeri razionali, cioè dei numeri
della forma m/n, con m ed n interi (ed n diverso da zero). In effetti
tra due numeri razionali qualsiasi esistono