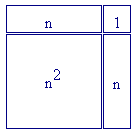
Lo si vede subito dal seguente disegnino, che rappresenta un quadrato di lato n+1:
A prima vista sembra banalmente che esistano infinite terne pitagoriche: infatti, se x, y e z soddisfano la (E1.1), anche nx, ny ed nz (con n intero) la soddisfano. Escludiamo questa soluzione banale del nostro problema e chiediamoci se esistono infinite terne NON proporzionali tra di loro che soddisfano la nostra relazione (il che equivale, dal punto di vista geometrico, a considerare 'uguali' triangoli rettangoli simili e nel chiedersi se esistono infiniti triangoli rettangoli non simili tra di loro e con i lati tutti esprimibili da numeri interi).
Lo si vede subito dal seguente disegnino, che rappresenta un quadrato di lato n+1:

| x = m2 - n2 |
| y = 2mn |
cosa che implica
| z = m2 + n2 |
con m ed n interi positivi con m>n. Per evitare di trovare terne tra loro proporzionali occorre anche richiedere che m ed n siano primi fra loro e non entrambi dispari (ad esempio, la soluzione con m=2 ed n=1 Ŕ proporzionale a quella con m=3 ed n=1).