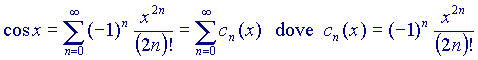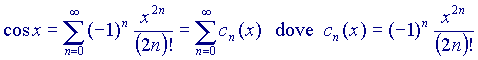
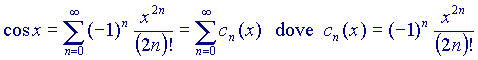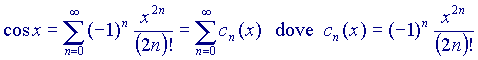
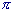 e calcoliamo i primi elementi della serie, ponendo
e calcoliamo i primi elementi della serie, ponendo 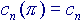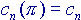 :
:
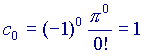
(ricordo che a0=1 e che 0!=1 per ogni a)
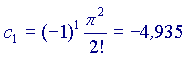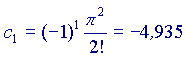
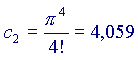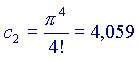
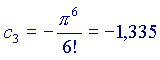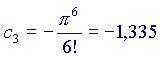
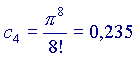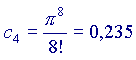
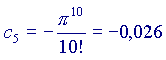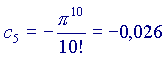
Ora,
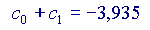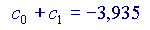
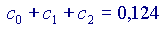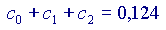
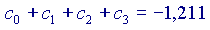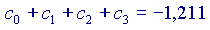
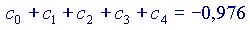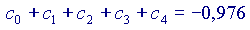
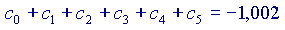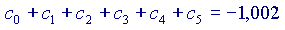
Si vede che ogni volta che si aggiunge un addendo alla somma, il risultato si avvicina sempre di più al valore 'vero' della nostra funzione, cioè a 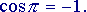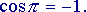 Volendo, si potrebbe provare anche con altri valori di x, diversi da
Volendo, si potrebbe provare anche con altri valori di x, diversi da 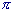 , ottenendo sempre una buona approssimazione già dopo pochi passi. Allo stesso modo si possono controllare (non 'dimostrare', ovviamente!) anche le altre espressioni. Ci accontentiamo di questo per considerare validi questi sviluppi in serie.
, ottenendo sempre una buona approssimazione già dopo pochi passi. Allo stesso modo si possono controllare (non 'dimostrare', ovviamente!) anche le altre espressioni. Ci accontentiamo di questo per considerare validi questi sviluppi in serie.
╚ proprio qui che stiamo barando, come del resto barava Eulero: questa Ŕ in effetti una tipica tecnica di dimostrazione formale del XVIII secolo. Occorre in realtÓ giustificare la sostituzione di x reale con ix immaginario, e per fare questo Ŕ necessaria la teoria delle funzioni di variabile complessa, una delle grandi conquiste del XIX secolo. Noi comunque, con Eulero, ci accontentiamo. Siamo in buona compagnia...
Home