sono compresi, oltre ai numeri interi ed ai numeri razionali, anche i numeri irrazionali, come 
.
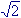Questo elegante procedimento (a quanto ne so inventato da Cantor) si chiama diagonalizzazione proprio perché si modifica l'n-esima cifra dell'n-esimo numero. Tale procedimento verrà spesso utilizzato dopo di lui, ad esempio anche da Gödel nella sua notevole dimostrazione del teorema sull'indecidibiltà.
Vogliamo trovare S tale che:
Moltiplichiamo ambo i membri della precedente uguaglianza per q:
da cui si trova:
valida per ogni k e per ogni q. Se k
Nel nostro caso q=1/10 e S=1/9, come detto.
da cui si ricava, ad esempio (ricordo che a-b=1/ab):
Si intende così cosa significa affermare che un numero decimale con infiniti 9 dopo la virgola è un numero razionale.
I risultati di Gödel-Cohen e le loro successive generalizzazioni comportano che non esiste una teoria degli insiemi, ma molte, diverse, in relazione a un problema a proposito del quale l'intuizione sembra ancora suggerirci che 'in realtà' debba esistere una sola soluzione vera.
(Corsivo mio. Vedi a pag. 43 del Quaderno de Le Scienze n. 92 dell'ottobre 1996, dove si trova anche, a pag.54, un interessante articolo dello stesso Cohen: La teoria non cantoriana degli insiemi).
.
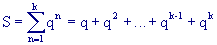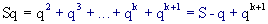
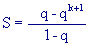
questa somma converge a un valore finito se e solo se qk+10, e in questo caso:
.
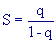Piccola osservazione che non c'entra nulla col discorso degli insiemi non numerabili, ma che è interessante di suo: se nella somma si parte non da 1 ma da m, si dimostra in un attimo che
.
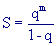
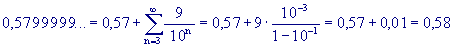Aggiungo solo che, se al posto di 1/10n si circondano i razionali tra 0 ed 1 con intervalli lunghi 
/10n con piccolo a piacere, si può rendere questa somma vicina a 0 quanto si vuole. In teoria della misura si esprime questo fatto dicendo che un insieme numerabile di punti è a misura nulla.
Con sua stessa sorpresa: in una lettera del 1877 scrive: Lo vedo, ma non lo credo!
Semplicemente 'alternando' le cifre dello sviluppo decimale dei due numeri reali che identificano un punto della superficie per ottenere un numero reale che identifica un punto nel segmento.
Tale ragionamento si estende senza alcuna difficoltà a superfici di dimensione n qualunque; pertanto l'insieme dei punti di qualsiasi spazio con un numero finito di dimensioni è equivalente all'insieme dei punti di un segmento.
La topologia ha come oggetto lo studio delle proprietà delle figure geometriche che persistono anche quando le figure sono sottoposte a deformazioni così profonde da perdere tutte le loro proprietà metriche e proiettive. Per chiarire questi concetti, possiamo dire che il fatto che un triangolo sia equilatero è una proprietà metrica del triangolo (perché comporta affermazioni sulla lunghezza dei suoi lati), mentre il fatto di essere un triangolo è una proprietà proiettiva (infatti un triangolo rimane tale anche quando lo si proietta su un piano differente). Topologicamente succede un po' di tutto: un triangolo è topologicamente equivalente ad un quadrato, o anche ad un'ellisse, perché è possibile deformarlo con continuità per ottenere appunto queste figure.
Serie infinita perché una volta ottenuto P(D) posso creare il suo insieme potenza P', e da questo il suo insieme potenza P'', ecc...
'Essenzialmente differenti' perché appunto non esiste alcuna relazione biunivoca tra gli elementi di D e quelli di P(D), quindi i due insiemi non sono equivalenti tra loro secondo la definizione di Cantor.
A questo proposito il logico A. Church, nell'assegnare nel 1966 un importante premio a P. Choen, proprio in relazione al suo contributo alla soluzione (o meglio alla 'irrisoluzione') del problema del continuo, affermava tra l'altro:
Molti matematici, oggi, sperano però che si possa trovare un nuovo assioma della teoria, evidente per se stesso, nel senso che tutti i matematici siano d'accordo nel considerarlo 'vero', tale che con questa aggiunta sia possibile dimostrare la verità o la falsità dell'ipotesi del continuo.
Home