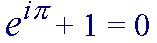Questa elegante formula, dovuta ad Eulero, grande matematico svizzero del XVIII secolo, stabilisce una relazione apparentemente strabiliante tra alcune costanti di utilizzo universale: a prima vista sembra davvero molto strano che 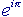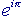 (un numero trascendente elevato all'unità immaginaria moltiplicata per un altro numero trascendente...) possa essere uguale a -1, no?
(un numero trascendente elevato all'unità immaginaria moltiplicata per un altro numero trascendente...) possa essere uguale a -1, no?
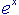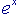 che qui riporto:
che qui riporto:
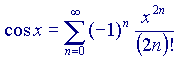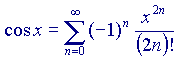
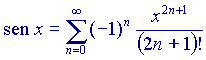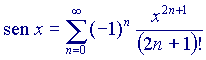
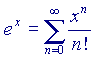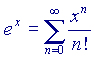
Queste formule non sono temibili come sembrano; rappresentano un'approssimazione tramite funzioni polinomiali in x (sono cioè funzioni delle potenze di x) di funzioni che polinomiali non sono. La dimostrazione della validità di questi sviluppi in serie passa attraverso teoremi che utilizzano strumenti tipici del calcolo differenziale e, anche qui, il tutto sembra molto più difficile di quanto sia in realtà (tra parentesi, è abbastanza evidente che al crescere di n il valore assoluto dei singoli addendi diventi sempre più piccolo - in effetti, per n sufficientemente grande, n! cresce molto più rapidamente di  qualunque sia x - mentre non è affatto evidente che la somma di questi infiniti addendi, che pur singolarmente tendono a zero, converga infine verso un valore finito, e per di più proprio uguale a quello della funzione desiderata. Per dimostrare questo ci vogliono appunto i teoremi citati poco sopra).
qualunque sia x - mentre non è affatto evidente che la somma di questi infiniti addendi, che pur singolarmente tendono a zero, converga infine verso un valore finito, e per di più proprio uguale a quello della funzione desiderata. Per dimostrare questo ci vogliono appunto i teoremi citati poco sopra).
Ora torniamo alla formula di Eulero. Osservando che 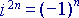 è facile rendersi conto che:
è facile rendersi conto che:
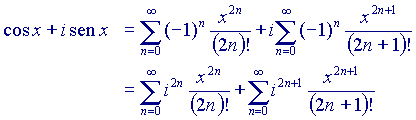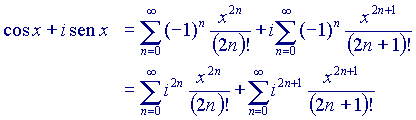
Ora, la prima somma è condotta sui numeri pari e la seconda sui numeri dispari, mentre l'addendo è sempre lo stesso. Possiamo quindi scrivere, più semplicemente:
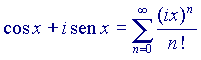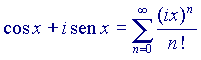
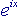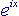 , quindi infine possiamo scrivere (barando un po'...):
, quindi infine possiamo scrivere (barando un po'...):
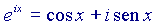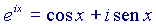
che è la formula generale, dovuta appunto ad Eulero, che lega le funzioni trigonometriche ed esponenziali. Da questa, ponendo  e sapendo che
e sapendo che  , segue direttamente quanto volevamo dimostrare.
, segue direttamente quanto volevamo dimostrare.
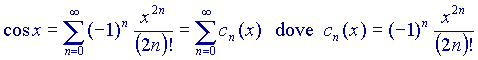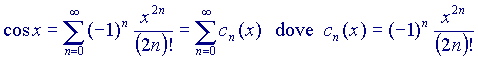
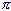 e calcoliamo i primi elementi della serie, ponendo
e calcoliamo i primi elementi della serie, ponendo 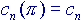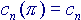 :
:
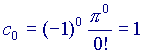
(ricordo che a0=1 e che 0!=1 per ogni a)
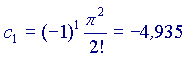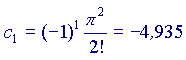
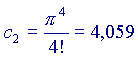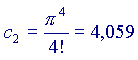
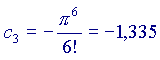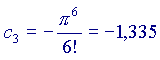
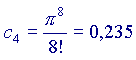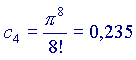
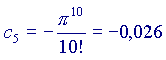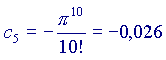
Ora,
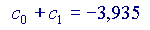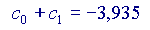
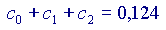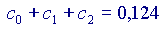
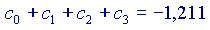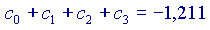
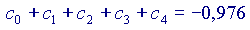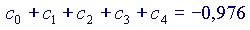
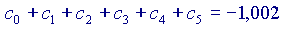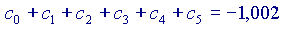
Si vede che ogni volta che si aggiunge un addendo alla somma, il risultato si avvicina sempre di più al valore 'vero' della nostra funzione, cioè a 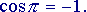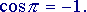 Volendo, si potrebbe provare anche con altri valori di x, diversi da
Volendo, si potrebbe provare anche con altri valori di x, diversi da 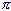 , ottenendo sempre una buona approssimazione già dopo pochi passi. Allo stesso modo si possono controllare (non 'dimostrare', ovviamente!) anche le altre espressioni. Ci accontentiamo di questo per considerare validi questi sviluppi in serie.
, ottenendo sempre una buona approssimazione già dopo pochi passi. Allo stesso modo si possono controllare (non 'dimostrare', ovviamente!) anche le altre espressioni. Ci accontentiamo di questo per considerare validi questi sviluppi in serie.