Insiemi non numerabili
Abbiamo visto come Cantor affronta il problema dell'infinito: afferma che due insiemi infiniti sono equivalenti quando tra i due insiemi esiste una relazione biunivoca (cioè una relazione che associa ad ogni elemento di un insieme uno ed un solo elemento dell'altro). Gli insiemi che abbiamo considerato erano tutti, più o meno ovviamente, numerabili, cioè si poteva trovare per ognuno di questi insiemi una relazione biunivoca con ![]() , l'insieme dei numeri naturali: vediamo ora un esempio di un insieme non numerabile.
, l'insieme dei numeri naturali: vediamo ora un esempio di un insieme non numerabile.
L'insieme dei numeri reali
Dopo aver dimostrato che
Cantor procede per assurdo, e assume che di fatto esista una successione numerabile di numeri reali, che li comprenda tutti. Assumiamo cioè che ![]() sia numerabile. A maggior ragione saranno numerabili i numeri reali compresi tra 0 ed 1. Sia f(n) la relazione biunivoca che fa corrispondere ad ogni n
sia numerabile. A maggior ragione saranno numerabili i numeri reali compresi tra 0 ed 1. Sia f(n) la relazione biunivoca che fa corrispondere ad ogni n![]()
![]() un f(n)
un f(n)![]()
![]() con 0<f(n)<1 e questi f(n) 'esauriscano' tutti i numeri reali compresi tra zero ed uno. Sia fm(n) la m-esima cifra dopo la virgola di f(n).
Applichiamo ora la diagonalizzazione, cioè costruiamo un numero che abbia come n-esima cifra dopo la virgola fn(n)+1: si vede subito che questo nuovo numero non può essere compreso tra gli f(n) che avevamo supposto esaurire tutti i numeri reali tra 0 ed 1, infatti ne differisce almeno per l'n-esima cifra! Questa contraddizione dimostra che non si possono porre in relazione biunivoca i numeri reali con i numeri naturali, quindi si deve porre:
con 0<f(n)<1 e questi f(n) 'esauriscano' tutti i numeri reali compresi tra zero ed uno. Sia fm(n) la m-esima cifra dopo la virgola di f(n).
Applichiamo ora la diagonalizzazione, cioè costruiamo un numero che abbia come n-esima cifra dopo la virgola fn(n)+1: si vede subito che questo nuovo numero non può essere compreso tra gli f(n) che avevamo supposto esaurire tutti i numeri reali tra 0 ed 1, infatti ne differisce almeno per l'n-esima cifra! Questa contraddizione dimostra che non si possono porre in relazione biunivoca i numeri reali con i numeri naturali, quindi si deve porre:
Qui si scrive C per rappresentare la cardinalità di ![]() perché si dice che
perché si dice che ![]() ha la 'potenza del continuo', dove continuo è un altro nome dato all'insieme dei numeri reali. Si può giustificare tale nome con il fatto che i numeri reali coprono 'davvero', in modo 'continuo', la retta dei numeri. Si può in effetti utilizzare questa proprietà (che apparentemente anche i numeri razionali posseggono) per mostrare in modo a mio avviso spettacolare come in effetti i numeri reali siano davvero 'di più' dei numeri razionali. Si procede così:
ha la 'potenza del continuo', dove continuo è un altro nome dato all'insieme dei numeri reali. Si può giustificare tale nome con il fatto che i numeri reali coprono 'davvero', in modo 'continuo', la retta dei numeri. Si può in effetti utilizzare questa proprietà (che apparentemente anche i numeri razionali posseggono) per mostrare in modo a mio avviso spettacolare come in effetti i numeri reali siano davvero 'di più' dei numeri razionali. Si procede così:
In modo intuitivo possiamo senz'altro affermare che il segmento di retta da 0 ad 1 'è lungo' 1. Se prendiamo tutti i numeri razionali compresi tra 0 ed 1 e 'racchiudiamo' ciascun numero razionale in un piccolo intervallino, viene naturale aspettarsi che, sommando la lunghezza di ognuno di questi intervallini (eventualmente sovrapponentisi), si ottenga infine almeno 1 come risultato. E invece no: proviamo a 'racchiudere' l'n-esimo numero razionale in un intervallino di lunghezza 1/10n. Sommiamo ora questi intervallini: si vede che:
Insomma, i numeri razionali tra zero ed uno, pur essendo infiniti, sono 'così pochi' che, anche se ciascuno di loro viene 'circondato' da un intervallino di lunghezza non nulla, non riescono a 'ricoprire' per intero il segmento di lunghezza unitaria! Questo è il punto di partenza della cosidetta teoria della misura, della quale non diremo altro.
Ora ci si potrebbe aspettare che i punti di una superficie, ad esempio del quadrato di lato 1, siano 'di più' di quelli di un segmento, ma Cantor riuscì a porre questi due insiemi di punti in corrispondenza biunivoca.
Viene da chiedersi a questo punto cosa vuol dire che il segmento ha dimensione 1 e una superficie dimensione 2, se questi due insiemi di punti sono equivalenti. In effetti quello di dimensione è un concetto topologico (che non approfondiremo) per cui è importante la continuità della corrispondenza tra i punti: una figura A è topologicamente equivalente a B se esiste una corrispondenza biunivoca tra i punti di A e quelli di B e se tale corrispondenza è continua, cioè se punti in A la cui distanza tende a zero vengono trasformati in punti di B la cui distanza tende pure a zero e viceversa. È quest'ultima condizione di continuità che non viene soddisfatta dalla corrispondenza biunivoca trovata da Cantor che stabilisce l'equivalenza tra una superficie ed un segmento.
Quindi l'equivalenza nel senso della teoria degli insiemi non è equivalenza topologica. In effetti non esistono due figure di dimensioni diverse che siano equivalenti topologicamente (e questo è un teorema, detto della 'invarianza della dimensionalità').
I numeri cardinali transfiniti
Cantor, ancora utilizzando il suo metodo diagonale, con il quale aveva già dimostrato la non numerabilità di ![]() , dimostra anche il seguente fatto notevole:
, dimostra anche il seguente fatto notevole:
| L'insieme P(D) formato da tutti i sottoinsiemi di un insieme dato D non si può porre in relazione biunivoca con D. |
Questo è banalmente vero per D finito, ma Cantor dimostra questo risultato anche per D infinito. L'insieme P(D) si chiama insieme potenza di D, e quindi per ogni insieme D vale:
Dunque Cantor dimostra che non esistono i soli due 'tipi' di infinito che avevamo indicato con ![]() e con C, ma addirittura una serie infinita di modi essenzialmente differenti di 'essere infinito'. Chiaramente, il solito simbolo
e con C, ma addirittura una serie infinita di modi essenzialmente differenti di 'essere infinito'. Chiaramente, il solito simbolo ![]() è insufficiente a rappresentarli tutti... Tali 'modi' di essere infinito si indicano con:
è insufficiente a rappresentarli tutti... Tali 'modi' di essere infinito si indicano con:
e questi strani oggetti si chiamano numeri cardinali transfiniti di Cantor.
L'ipotesi del continuo
Viene naturale chiedersi a quale numero cardinale transfinito corrisponda C: sicuramente non adSi può cioè dire che non esistono cardinali transfiniti 'intermedi' tra
Questa è la famosa ipotesi del continuo, che Cantor tentò in tutti i modi di dimostrare. Non ci riuscì e consegnò la questione ai suoi successori e la storia è abbastanza interessante: nel 1900 Hilbert cita questo problema come primo di una lista di problemi irrisolti la cui soluzione avrebbe rappresentato un significativo avanzamento delle conoscenze matematiche; nel 1938 Gödel dimostra che se la teoria degli insiemi senza l'ipotesi del continuo è consistente, lo è anche la teoria che si ottiene aggiungendo tale ipotesi come 'assioma' aggiuntivo e P. Cohen dimostra nel 1963 che si trovano nella stessa situazione anche le teorie che si ottengono negando l'ipotesi del continuo!
In definitiva, si può riguardare l'ipotesi del continuo più o meno alla stessa stregua del famoso postulato delle parallele di Euclide: in sé tali affermazioni non sono né vere né false e così come negando il postulato delle parallele si ottengono le geometrie non euclidee, negando l'ipotesi del continuo si ottengono delle teorie degli insiemi che si possono dire 'non cantoriane'.
Non si sa ancora se tali teorie 'non cantoriane' avranno implicazioni importanti nello sviluppo della matematica e delle scienze fisiche: viene però naturale osservare che alla base della teoria della relatività generale di Einstein, con il suo spazio-tempo curvo, c'è la geometria non euclidea... forse possiamo aspettarci qualcosa di interessante dalle teorie non cantoriane degli insiemi!
 sono compresi, oltre ai numeri interi ed ai numeri razionali, anche i numeri irrazionali, come
sono compresi, oltre ai numeri interi ed ai numeri razionali, anche i numeri irrazionali, come 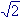 .
.
Vai alla pagina relativa
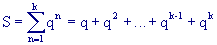 .
.
Moltiplichiamo ambo i membri della precedente uguaglianza per q:
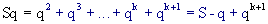
da cui si trova:
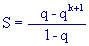
valida per ogni k e per ogni q. Se k
 questa somma converge a un valore finito se e solo se qk+1
questa somma converge a un valore finito se e solo se qk+1 0, e in questo caso:
0, e in questo caso:
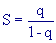 .
.
Nel nostro caso q=1/10 e S=1/9, come detto.
Piccola osservazione che non c'entra nulla col discorso degli insiemi non numerabili, ma che è interessante di suo: se nella somma si parte non da 1 ma da m, si dimostra in un attimo che
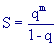
da cui si ricava, ad esempio (ricordo che a-b=1/ab):
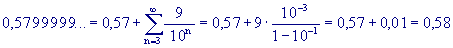 .
.
Si intende così cosa significa affermare che un numero decimale con infiniti 9 dopo la virgola è un numero razionale.
 /10n con
/10n con  piccolo a piacere, si può rendere questa somma vicina a 0 quanto si vuole. In teoria della misura si esprime questo fatto dicendo che un insieme numerabile di punti è a misura nulla.
piccolo a piacere, si può rendere questa somma vicina a 0 quanto si vuole. In teoria della misura si esprime questo fatto dicendo che un insieme numerabile di punti è a misura nulla.
Tale ragionamento si estende senza alcuna difficoltà a superfici di dimensione n qualunque; pertanto l'insieme dei punti di qualsiasi spazio con un numero finito di dimensioni è equivalente all'insieme dei punti di un segmento.
|
I risultati di Gödel-Cohen e le loro successive generalizzazioni comportano che non esiste una teoria degli insiemi, ma molte, diverse, in relazione a un problema a proposito del quale l'intuizione sembra ancora suggerirci che 'in realtà' debba esistere una sola soluzione vera. |
(Corsivo mio. Vedi a pag. 43 del Quaderno de Le Scienze n. 92 dell'ottobre 1996, dove si trova anche, a pag.54, un interessante articolo dello stesso Cohen: La teoria non cantoriana degli insiemi).
Molti matematici, oggi, sperano però che si possa trovare un nuovo assioma della teoria, evidente per se stesso, nel senso che tutti i matematici siano d'accordo nel considerarlo 'vero', tale che con questa aggiunta sia possibile dimostrare la verità o la falsità dell'ipotesi del continuo.