Infinità delle terne pitagoriche
Il problema è dimostrare se esistono o no infinite terne di numeri interi che soddisfino la relazione:
| (E1.1) | x2 + y2 = z2. |
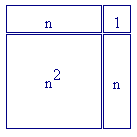
Ora, è facile convincersi che la differenza tra due quadrati consecutivi è un numero dispari: per la precisione
(n+1)2 - n2 = 2n + 1.
Ma fra gli infiniti numeri dispari, ve ne sono infiniti che sono quadrati a loro volta (banalmente, i quadrati dei numeri dispari...). Cioè, esistono infiniti m per cui è vero che
m2 = 2n + 1.
Ora, poiché 2n+1 è la differenza tra due quadrati consecutivi, possiamo scrivere
m2 = (n+1)2 - n2
e cioè esistono infiniti m dispari - e relativi n = (m2 - 1)/2 - per cui
m2 + n2 = (n+1)2.
Euclide conclude quindi che esistono infinite terne pitagoriche. Carino, no?
Si dimostra la seguente soluzione generale: le possibilità di formare terne pitagoriche sono esaurite da x e y della forma:
| x = m2 - n2 |
| y = 2mn |
cosa che implica
| z = m2 + n2 |
con m ed n interi positivi con m>n. Per evitare di trovare terne tra loro proporzionali occorre anche richiedere che m ed n siano primi fra loro e non entrambi dispari (ad esempio, la soluzione con m=3 ed n=1 è proporzionale a quella con m=2 ed n=1).